Еднаквости в равнината

1.1. Осева симетрия

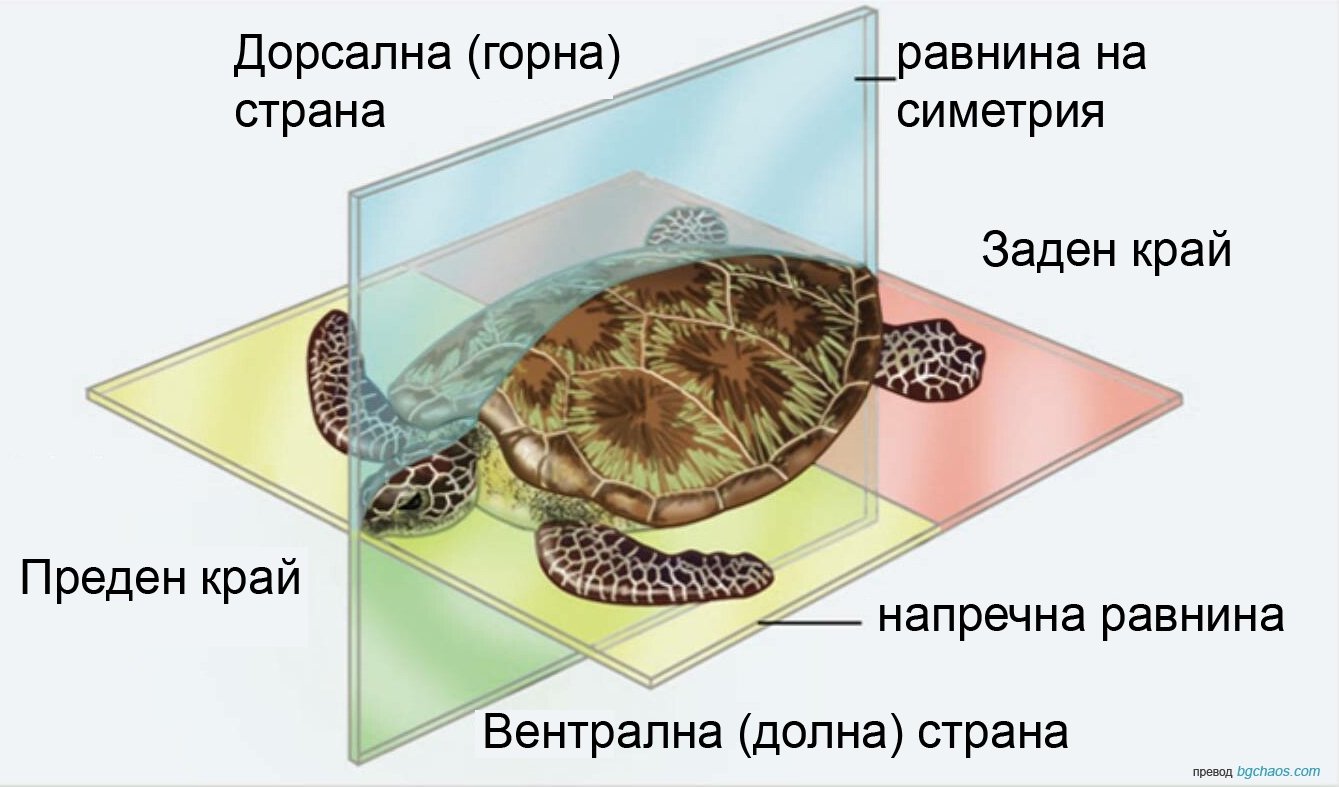
Определение. Нека σ е права. Осева симетрия (огледална симетрия) с ос σ се нарича еднаквост, за която всяка точка от σ е неподвижна и която и да е полуравнина с граница σ се изобразава в другата полуравнина със същата граница.

илюстрация за осева симетрия следният витраж от оцветено стъкло:

Приложение на осевата симетрия в живота

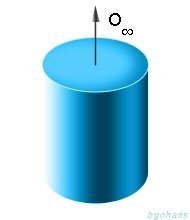
Тялото има ос на симетрия n-ти ред Оn, ако при въртене около тази ос, тялото n пъти съвпада със себе си, а завъртанията са 360°/n. Самата операция на симетрия се бележи със Cn , където n e порядъкът на симетрия.Ако едно тяло съвпада само със себе си, когато се завърта на какъвто и да е ъгъл, такова тяло се нарича осевосиметрично, а правата, около която се извършва завъртането на произволен ъгъл се нарича ос на симетрия. В този случай оста на симетрия може да се разглежда като ос на симетрия от безкраен ред O∞ и се превръща в пределна група.Най-простата пространствена фигура, която има ос на симетрия от безкраен ред O∞, е цилиндърът, затова този тип симетрия се нарича още цилиндрична симетрия.

Задачи за Осева симетрия:1зад:Точката X' е образ на X при осева симетрия. Постройте образа на произволна точка Y при същата симетрия.

2зад:Докажете, че правоъгълника е симетрична фигура с оси на симетрията правите, съединяващи средите на срещуположните страни.

3зад:Докажете, че ромбът е симетрична фигура с оси на симетрия всеки от диагоналите му.

4зад:Докажете, че ако един трапец е симетрична фигура, то той е равнобедрен.

Централна симетрия

Определение. Нека Z е произволна точка. Централна симетрия с център Z се нарича въртенето на равнината около Z на ъгъл 180°.

Горната дефиниция се опира на познаването на еднаквостта ротация (въртене).

На централната симетрия, обаче, може да се погледне и като на отражение спрямо точката Z (т.е., спрямо центъра на симетрията).

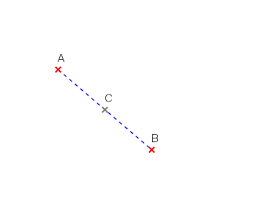
А именно: това е еднаквост, при която точката Z се изобразява в себе си, а образът на произволна точка P е такава точка P₁, че точката Z е среда на отсечката PP₁.

Друга интересна илюстрация на централната симетрия (макар и в тримерен вариант, а не в равнината) е така наречената камера обскур

Приложение на Централната симетрия в живота

Централна симетрия в природата симетрия може да се намери навсякъде, ако се вгледате внимателно към реалността около нас.Той присъства в снежинки, листа от дървета и цветя, трева, насекоми и животни.Централният симетрията на растения и живи организми напълно се определи въздействието на външната среда, които все още се формира прикритието на жители на планетата Земя.

Забелязваме симетрията и при насекомитеПеперуди, водни кончета - като анимирани цветя и развяващи.Изящните хищници и домашни котки ... може безкрайно да се възхищават на творенията на природата.

През дългата си история, от древни храмове и средновековни крепости на съвременния човек да разберат красотата, хармонията на създаване и изследвани чрез наблюдаване на природата.Urban свят, в който той живее по-голямата част от населението на Земята е пълна с симетрия.Този домакински уреди, предмети от бита, науката и изкуствата.Аналогия - успеха на всяка инженерна структура.

Свойства

Отсечка се изобразява в равна на нея.
Всяка права, която не минава през центъра, се изобразява в права, успоредна на дадената.
Ъгъл се изобразява в равен на него.
Фигура и нейният образ при централна симетрия са еднакви.
Централносиметрични фигури(фигури, които при централна симетрия с център О, се изобразяват в себе си)
- Отсечка; – среда
- Равностранен триъгълник; – център
- Успоредници:
  - Успоредник; - пресечната точка на диагоналите
  - Правоъгълник; - пресечната точка на диагоналите
  - Ромб; - пресечната точка на диагоналите
  - Квадрат; - пресечната точка на диагоналите
- Окръжност, – център на окръжността

Задачи за Централна симетрия:

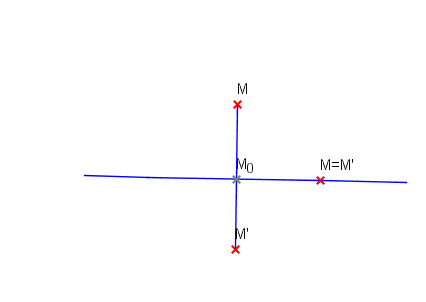
1зад:Дадени са права g, окръжност k(O;r) и точка S. Върху права g да се построи точка M', образ на точка от окръжността k при симетрия Ss. Да се построи и първообразът на M'

2зад:Дадени са окръжност k(O;r) и k'(O';r') и точка S. Да се построи отсечка, краищата на която да лежат съответно върху окръжностите k и k'', да минава през точка S и да се разполовява от нея.

3зад:Даден е триъгълник ABC с периметър 2p и точка M. Точките A' B' C' са симетрични на М относно средите на страните на ABC. Намерете периметъра на триъгълника A' B' C'.

1.3. Ротация

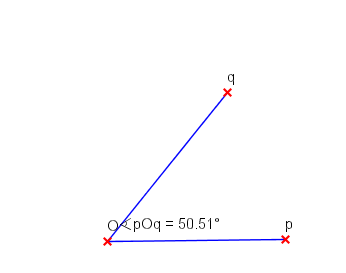
Насочен ъгъл – ъгъл, на който едното рамо е прието за първо (начално), а другото за второ (крайно), е насочен (ориентиран) ъгъл.В равнината има две посоки на въртене на лъчите около точка. Посоката, обратна на движението на часовниковата стрелка, е приета за положителна, а другата – за отрицателна. Насоченият ъгъл бива положителен или отрицателен, ако завъртането на началното му рамо, до съвпадането му с второто, като се минава през вътрешността на ъгъла, е съответно положително или отрицателно.Ротация – определение: Геометрично преобразувание, при което на всяка точка X, различна от О, съответства точка X1, такава, че OX=OX1 и ∠XOX1=α, а на точка O съответства самата точка О, се нарича ротация (въртене) с център O на ъгъл α. Бележим с ρ(O; α). Ако точка X1 e образ на точка X, пишем X1 = ρ(X) или ρ(O; α): X→X1

Може да се докаже, че при ротация:

права се изобразява в права
отсечка се изобразява в отсечка
лъч се изобразява в лъч
окръжност се изобразява в окръжност

Следователно, за да намерим образа на отсечка или права, достатъчно е да намерим образите на краищата на отсечката или образите на две точки от правата.
Основно свойство на ротацията: Ротацията запазва разстоянието между точките.
Оттук следва, че при ротацията:

отсечка се изобразява в равна на нея отсечка
триъгълник се изобразява в еднакъв на него триъгълник
ъгъл се изобразява в равен на него ъгъл
окръжност се изобразява в еднаква на нея окръжност

Не е трудно да се съобрази, че при ротация права и образът и сключват ъгъла на въртене.

Друга илюстрация на ротацията е следната снимка, на реалното квантово-механично явление "entanglement" на орбиталния ъглов момент на фотоните, излъчени от лазерен източник

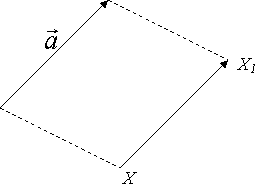
1.4. Транслация ::Нека е дадена точка X и вектор а. Знаем, че съществува единствена точка X1 в равнината така, че вектор XX1 е равен на вектор а

Определение: Геометрично преобразувание, при което на всяка точка X се съпоставя точка X₁ такава,че вектор XX₁ = вектор а, се нарича транслация (успоредно пренасяне) на вектор а.
Означаваме с τ_а и пишем X₁ = τ_а(X) или τ_а : X → X₁, X₁ е образът на точката X при тази транслация.
Вектор а се нарича вектор на транслацията.

Може да се докаже, че при транслацията:

права се изобразява в права
отсечка се изобразява в отсечка
лъч в лъч
окръжност в окръжност

Т. Транслацията запазва разстоянието между точките.

Оттук следва, че при транслацията:

две съответни отсечки са равни и успоредни или лежат на една права
две съответни прави са успоредни или съвпадат
два съответни ъгъла имат съответно успоредни рамене
два съответни триъгълника са еднакви и имат съответно успоредни страни

Можем да си представим как първата стъклена масичка е преместена на мястото на втората, а после и на мястото на третата. Векторът на транслация е по диагонала на квадрата, представляващ или горната повърхост, или основата на масичката.